Example #1: the excited electronic states of chlorine dioxide, OClO

K.A. Peterson and H.-J. Werner, J. Chem. Phys. 105, 9823 (1996)

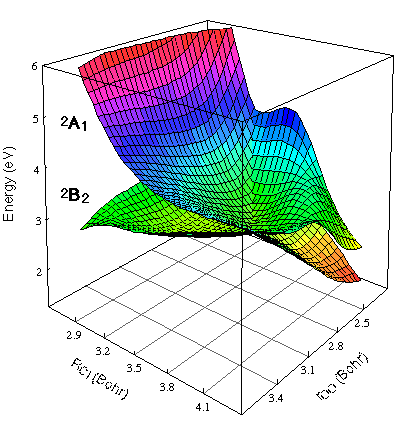
below: 2-dimensional cut for the ²A₁ and ²B₂ states restricting to C_2v symmetry (crossing allowed)

Note that the ²A₁ and ²B₂ states are allowed to (and indeed do) cross for these symmetric geometries and that the crossing is
really along a seam (line).

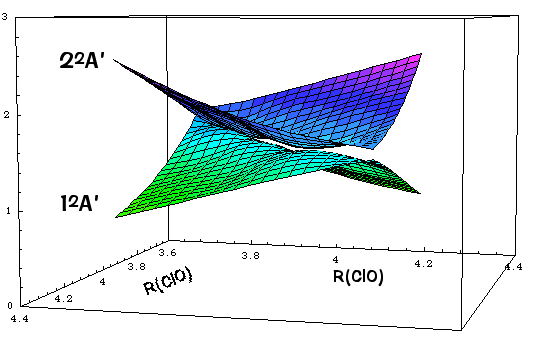
below: 2-dimensional cut for asymmetric bond length displacements

Note that the crossing is now avoided but the surfaces "touch" just at the C_2v (r₁ = r₂) geometries.

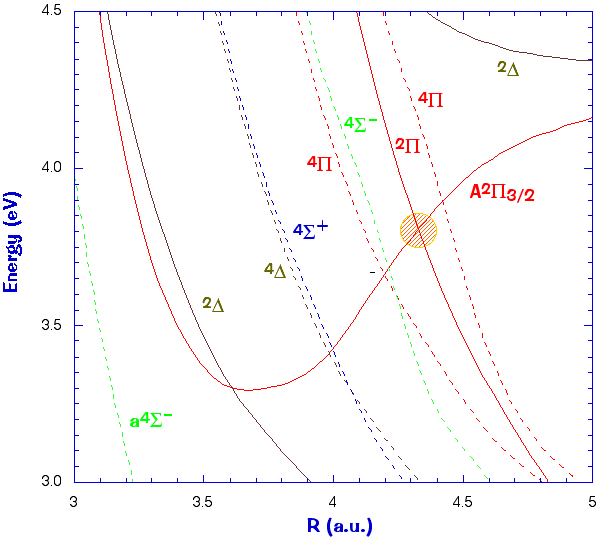
Example #2: the excited electronic states of the BrO radical

Note the crossing between the two states of the same symmetry, A²P (Pi) and 3²P (Pi), in the hashed region.
In this case the crossing is very narrowly avoided (it's actually depicted below like an allowed crossing) since
the two wavefunctions have very different electronic character. The other curves describe other electronic states
that are allowed to cross the "A" state (dashed lines are quartet states, solid lines are doublet states).

One can explicitly calculate the 1st-order non-adiabatic coupling matrix elements (NACME) as a function of the
internuclear distance R.
Note that the NACME is a very strong function of the internuclear distance and peaks at the crossing point

.

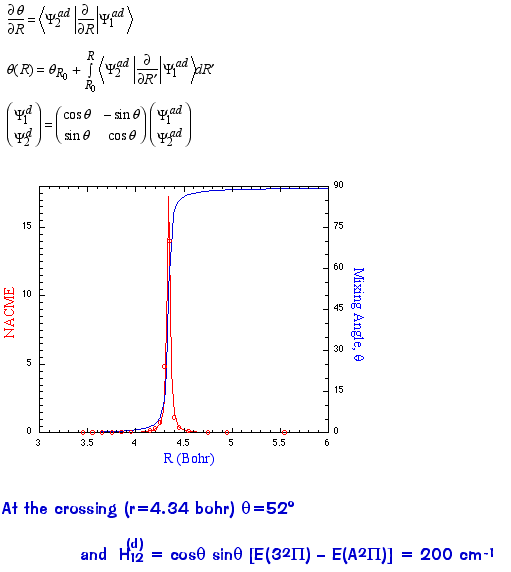
The NACME can be used to define what are called "diabatic" states (i.e., non-adiabatic) that differ from the usual "adiabatic"
states (i.e., eigenfunctions of the electronic H) in that their character varies smoothly through the crossing. For two states this
involves just a unitary transformation to the diabatic basis, i.e., just a rotation by the angle q (theta). In this basis the coupling
between the electronic states no longer appears in the nuclear kinetic energy term but only in the coordinates (potential energy
couplings only). The diabatic states are allowed to cross (but have explicit coupling matrix elements, e.g., the H₁₂ term above):